Attractor
An attractor is a set towards which a variable moving according to the dictates of a dynamical system evolves over time. That is, points that get close enough to the attractor remain close even if slightly disturbed. The evolving variable may be represented algebraically as an n-dimensional vector. The attractor is a region in n-dimensional space. In physical systems, the n dimensions may be, for example, two or three positional coordinates for each of one or more physical entities; in economic systems, they may be separate variables such as the inflation rate and the unemployment rate.
If the evolving variable is two- or three-dimensional, the attractor of the dynamic process can be represented geometrically in two or three dimensions, as for example in the three-dimensional case depicted to the right. An attractor can be a point, a finite set of points, a curve, a manifold, or even a complicated set with a fractal structure known as a strange attractor. If the variable is a scalar, the attractor is a subset of the real number line. Describing the attractors of chaotic dynamical systems has been one of the achievements of chaos theory.
A trajectory of the dynamical system in the attractor does not have to satisfy any special constraints except for remaining on the attractor. The trajectory may be periodic or chaotic. If a set of points is periodic or chaotic, but the flow in the neighbourhood is away from the set, the set is not an attractor, but instead is called a repeller (or repellor).
Contents |
Motivation
A dynamical system is generally described by one or more differential or difference equations. The equations of a given dynamic system specify its behavior over any given short period of time. To determine the system's behavior for a longer period, it is necessary to integrate the equations, either through analytical means or through iteration, often with the aid of computers.
Dynamical systems in the physical world tend to be dissipative: if it were not for some driving force, the motion would cease. (Dissipation may come from internal friction, thermodynamic losses, or loss of material, among many causes.) The dissipation and the driving force tend to combine to kill out initial transients and settle the system into its typical behavior. This one part of the phase space of the dynamical system corresponding to the typical behavior is the attractor, also known as the attracting section or attractee.
Invariant sets and limit sets are similar to the attractor concept. An invariant set is a set that evolves to itself under the dynamics. Attractors may contain invariant sets. A limit set is a set of points such that there exists some initial state that ends up arbitrarily close to the limit set (i.e. to each point of the set) as time goes to infinity. Attractors are limit sets, but not all limit sets are attractors: It is possible to have some points of a system converge to a limit set, but different points when perturbed slightly off the limit set may get knocked off and never return to the vicinity of the limit set.
For example, the damped pendulum has two invariant points: the point 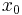 of minimum height and the point
of minimum height and the point 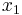 of maximum height. The point
of maximum height. The point 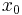 is also a limit set, as trajectories converge to it; the point
is also a limit set, as trajectories converge to it; the point 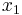 is not a limit set. Because of the dissipation, the point
is not a limit set. Because of the dissipation, the point 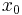 is also an attractor. If there were no dissipation,
is also an attractor. If there were no dissipation, 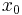 would not be an attractor.
would not be an attractor.
Mathematical definition
Let t represent time and let f(t, •) be a function which specifies the dynamics of the system. That is, if a is an n-dimensional point in the phase space, representing the initial state of the system, then f(0, a) = a and, for a positive value of t, f(t, a) is the result of the evolution of this state after t units of time. For example, if the system describes the evolution of a free particle in one dimension then the phase space is the plane R2 with coordinates (x,v), where x is the position of the particle, v is its velocity, a=(x,v), and the evolution is given by
An attractor is a subset A of the phase space characterized by the following three conditions:
- A is forward invariant under f: if a is an element of A then so is f(t,a), for all t > 0.
- There exists a neighborhood of A, called the basin of attraction for A and denoted B(A), which consists of all points b that "enter A in the limit t → ∞". More formally, B(A) is the set of all points b in the phase space with the following property:
-
- For any open neighborhood N of A, there is a positive constant T such that f(t,b) ∈ N for all real t > T.
- There is no proper subset of A having the first two properties.
Since the basin of attraction contains an open set containing A, every point that is sufficiently close to A is attracted to A. The definition of an attractor uses a metric on the phase space, but the resulting notion usually depends only on the topology of the phase space. In the case of Rn, the Euclidean norm is typically used.
Many other definitions of attractor occur in the literature. For example, some authors require that an attractor have positive measure (preventing a point from being an attractor), others relax the requirement that B(A) be a neighborhood.
Types of attractors
Attractors are parts of the phase space of the dynamical system. Until the 1960s, as evidenced by textbooks of that era, attractors were thought of as being simple geometrical subsets of the phase space: points, lines, surfaces, volumes. The (topologically) wild sets that had been observed were thought to be fragile anomalies. Stephen Smale was able to show that his horseshoe map was robust and that its attractor had the structure of a Cantor set.
Two simple attractors are the fixed point and the limit cycle. There can be many other geometrical sets that are attractors. When these sets (or the motions on them), are harder to describe than the classical geometric objects, then the attractor is a strange attractor, as described in the section below.
Fixed point
A fixed point is a point of a function that does not change under some transformation. If we regard the evolution of a dynamical system as a series of transformations, then there may or may not be a point which remains fixed under each transformation. The final state that a dynamical system evolves towards, such as the final states of a falling pebble, a damped pendulum, or the water in a glass, corresponds to an attracting fixed point of the evolution function, but the two concepts are not equivalent because not all fixed points attract the evolution of nearby points. A marble rolling around in a basin may have a fixed point, but if the marble is externally driven it may not be attracted to that fixed point. But in the absence of an external driving force, it will settle into the fixed point at the bottom of the bowl, so in this case that point is an attractor.
Limit cycle
- See main article limit cycle
A limit cycle is a periodic orbit of the system that is isolated. Examples include the swings of a pendulum clock, the tuning circuit of a radio, and the heartbeat while resting. (The limit cycle of an ideal pendulum is not an example of a limit cycle attractor because its orbits are not isolated: in the phase space of the ideal pendulum, near any point of a periodic orbit there is another point that belongs to a different periodic orbit, so the former orbit is not attracting).
Limit tori
There may be more than one frequency in the periodic trajectory of the system through the state of a limit cycle. If two of these frequencies form an irrational fraction (i.e. they are incommensurate), the trajectory is no longer closed, and the limit cycle becomes a limit torus. This kind of attractor is called an 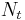 -torus if there are
-torus if there are 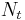 incommensurate frequencies. For example here is a 2-torus:
incommensurate frequencies. For example here is a 2-torus:
A time series corresponding to this attractor is a quasiperiodic series: A discretely sampled sum of 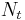 periodic functions (not necessarily sine waves) with incommensurate frequencies. Such a time series does not have a strict periodicity, but its power spectrum still consists only of sharp lines.
periodic functions (not necessarily sine waves) with incommensurate frequencies. Such a time series does not have a strict periodicity, but its power spectrum still consists only of sharp lines.
Strange attractor
An attractor is called strange if it has non-integer dimension. This is often the case when the dynamics on it are chaotic, but there also exist strange attractors that are not chaotic. The term was coined by David Ruelle and Floris Takens to describe the attractor that resulted from a series of bifurcations of a system describing fluid flow. Strange attractors are often differentiable in a few directions, but some are like a Cantor dust, and therefore not differentiable.
Examples of strange attractors include the Hénon attractor, Rössler attractor, Lorenz attractor, and Tamari attractor.
Partial differential equations
Parabolic partial differential equations may have finite-dimensional attractors. The diffusive part of the equation damps higher frequencies and in some cases leads to a global attractor. The Ginzburg–Landau, the Kuramoto–Sivashinsky, and the two-dimensional, forced Navier–Stokes equations are all known to have global attractors of finite dimension.
For the three-dimensional, incompressible Navier–Stokes equation with periodic boundary conditions, if it has a global attractor, then this attractor will be of finite dimensions.
Numerical localization (visualization) of attractors
From a computational point of view, attractors can be naturally regarded as self-exciting attractors or hidden attractors. Self-exciting attractors can be localized numerically by standard computational procedures, in which after a transient sequence, a trajectory starting from a point on an unstable manifold in a small neighborhood of an unstable equilibrium reaches an attractor (like classical attractors in the Van der Pol, Beluosov–Zhabotinsky, Lorenz, and many other dynamical systems). In contrast, the basin of attraction of a hidden attractor does not contain neighborhoods of equilibria, so the hidden attractor cannot be localized by standard computational procedures.
See also
References
- Attractor at Scholarpedia, curated by John Milnor.
- David Ruelle and Floris Takens (1971). "On the nature of turbulence". Communications of Mathematical Physics 20 (3): 167–192. doi:10.1007/BF01646553.
- D. Ruelle (1981). "Small random perturbations of dynamical systems and the definition of attractors". Communications of Mathematical Physics 82: 137–151. doi:10.1007/BF01206949.
- John Milnor (1985). "On the concept of attractor". Communications of Mathematical Physics 99 (2): 177–195. doi:10.1007/BF01212280.
- David Ruelle (1989). Elements of Differentiable Dynamics and Bifurcation Theory. Academic Press. ISBN 0-12-601710-7.
- Ruelle, David (August 2006). "What is...a Strange Attractor?" (PDF). Notices of the American Mathematical Society 53 (7): 764–765. http://www.ams.org/notices/200607/what-is-ruelle.pdf. Retrieved 2008-01-16.
- Ben Tamari (1997). Conservation and Symmetry Laws and Stabilization Programs in Economics. Ecometry ltd. ISBN 965-222-838-9.
- Grebogi, Ott, Pelikan, Yorke (1984). "Strange attractors that are not chaotic". Physica D 13: 261–268. doi:10.1016/0167-2789(84)90282-3.
Further reading
- Edward N. Lorenz (1996) The Essence of Chaos ISBN 0-295-97514-8
- James Gleick (1988) Chaos: Making a New Science ISBN 0-140-09250-1
External links
- Basin of attraction on Scholarpedia
- A gallery of trigonometric strange attractors
- Double scroll attractor Chua's circuit simulation
- A gallery of polynomial strange attractors
- Animated Pickover Strange Attractors
- Chaoscope, a 3D Strange Attractor rendering freeware
- 1D, 2D and 3D of strange attractors, include Tamari Attractor
- Research abstract and software laboratory
- Online strange attractors generator
- Tamari attractor
